通信中的符号同步

发表于 | 分类于

本篇主要学习一下符号同步相关的技术， 特别是timing 同步的环路， 这里的环路指的并不是PLL。

Timing 环路的构成

时间同步环路常由TED， 环路滤波器， VCO构成， 如下下图所示[1]:

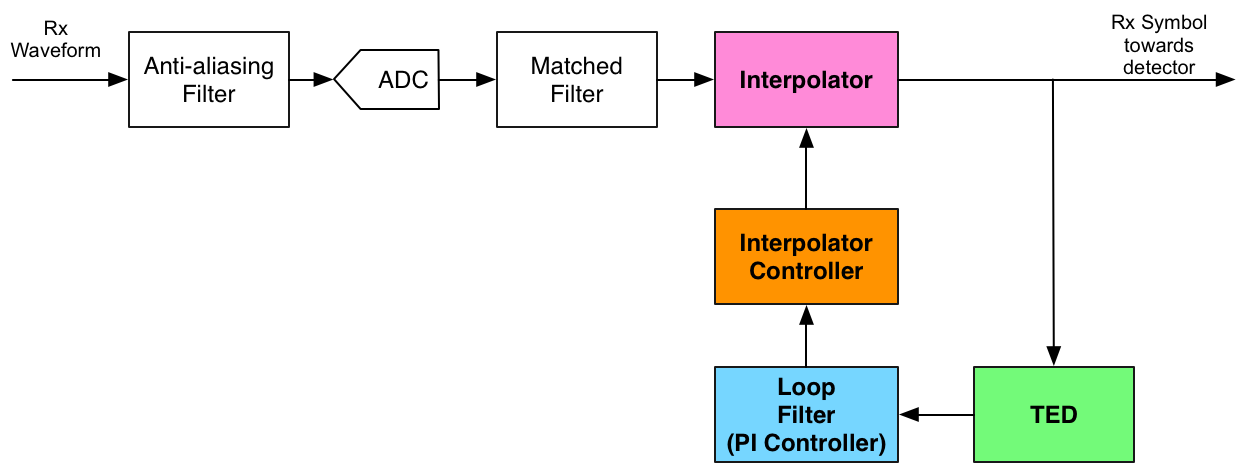
对于离散时间系统来说， 第n个接收到的符号可以用下面的模型来表示：

$T_s$是符号的周期， p 是信道的冲激响应， 对于上图中的模型来说， 包含了发端的pulse shape filter 和收端的match filter。

x(m) 代表的是第m个发送的符号， $v(nT_s)$这一项表示AWGN 噪声。

$\tau$ 代表的是范围在[0, $T_s$)内的timing 误差。 实际上由于信道的传输延时造成的timing error 可能由两部分构成：

a. 整数倍的$T_s$;

b. 小数倍的$T_s$;

对于timing loop来说， 我们关心的是小数倍的timing error， 而整数倍的timing error 可以由帧同步来修正。

TED

TED 的作用就是检测上文中提到的timing error $\tau$, 值得注意的是， 由于$\tau$ 的存在会有符号间的干扰， 常见的接收机结构是需要进行符号级的均衡后再进行判决。

Loop Filter

Loop Filter的基本概念就是能够决定修正timing error的快慢， 什么类型的timing error 可以被修正， 以及多大范围的时间误差可以被修正。

通常来说这部分是一个二阶系统， 可以看做是一个比例积分控制器(PI controller)

Interpolator

插值控制器对于timing loop 来说是很重要的一个组件。 比如， 过采样因子为L=4， 那么每一个symbol 的输出就会有L 个sample。那么接收机必须选择这4个sample 中的一个进行符号检测或者判决。

下面我们以PAM符号收发系统为例子， 用MATLAB详细说明timing 同步环路的作用

PAM 系统中的timing 同步

分三部分， 以MATLAB 代码和图片进行说明。

PAM的发送

如下所示：PAM 2 {+1， -1 ，+1， -1 …}符号产生

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
L        = 4;   % Oversampling factor
M         = 2;  % Pam Order
rollOff  = 0.5; % Pulse shaping roll-off factor
rcDelay  = 10;  % Raised cosine delay in symbols

% Arbitrary binary data
data          = zeros(1, 2*rcDelay);
data(1:2:end) = M-1;
% PAM-modulated symbols:
txSym         = real(pammod(data, M));

figure
stem(txSym)
title('Symbol Sequence')
xlabel('Symbol Index')
ylabel('Amplitude')

PAM 2符号为：

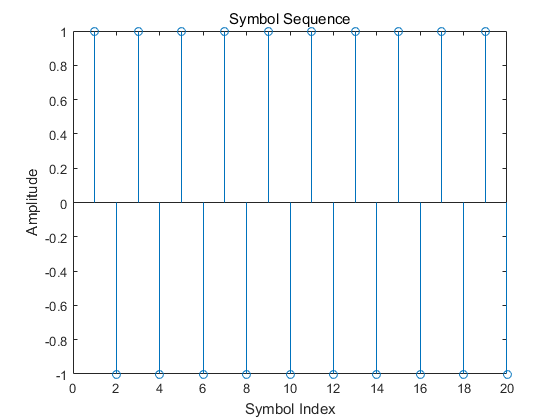
PAM2 4倍上采样后的sample为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
% Upsampling
txUpSequence = upsample(txSym, L);

figure
stem(txUpSequence)
title('Upsampled Sequence')
xlabel('Sample Index')
ylabel('Amplitude')

% Pulse Shaping
txSequence = filter(htx, 1, txUpSequence);

figure
stem(txSequence)
title('Shaped Transmit Sequence')
xlabel('Index')
ylabel('Amplitude')

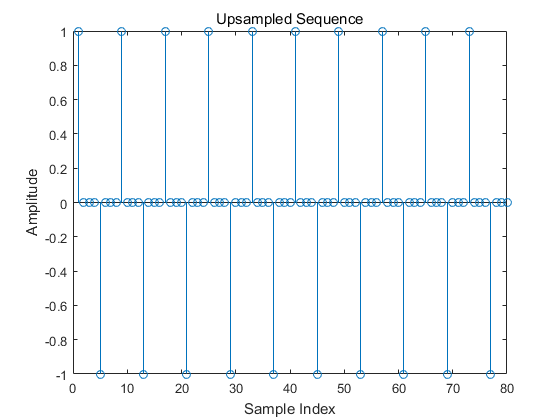
pulse shape

pulse shape 滤波器在发端symbol 产生之后， 用于频谱整形， 使之在通信标准的模板（Mask）之内. 以根升余弦滤波器为例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
L        = 4;         % Oversampling factor
rollOff  = 0.5;        % Pulse shaping roll-off factor
rcDelay  = 10;         % Raised cosine delay in symbols

% Filter:
htx = rcosine(1, L, 'sqrt', rollOff, rcDelay/2);
% Note half of the target delay is used, because when combined
% to the matched filter, the total delay will be achieved.
hrx  = conj(fliplr(htx));

figure
plot(htx)
title('Transmit Filter')
xlabel('Index')
ylabel('Amplitude')

figure
plot(hrx)
title('Rx Filter (Matched Filter)')
xlabel('Index')
ylabel('Amplitude')

p = conv(htx,hrx);

figure
plot(p)
title('Combined Tx-Rx = Raised Cosine')
xlabel('Index')
ylabel('Amplitude')

% And let's highlight the zero-crossings
zeroCrossings = NaN*ones(size(p));
zeroCrossings(1:L:end) = 0;
zeroCrossings((rcDelay)*L + 1) = NaN; % Except for the central index
hold on
plot(zeroCrossings, 'o')
legend('RC Pulse', 'Zero Crossings')
hold off

发端滤波器响应为：

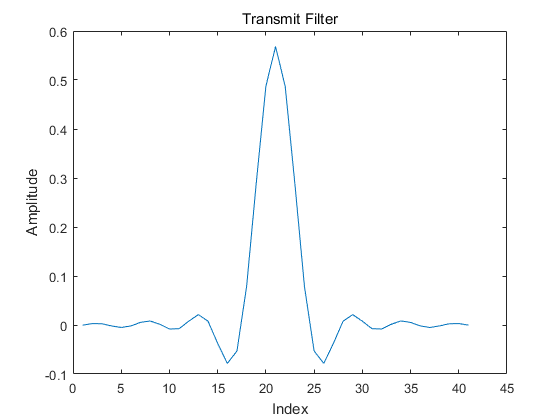
收端match filter 的响应为：

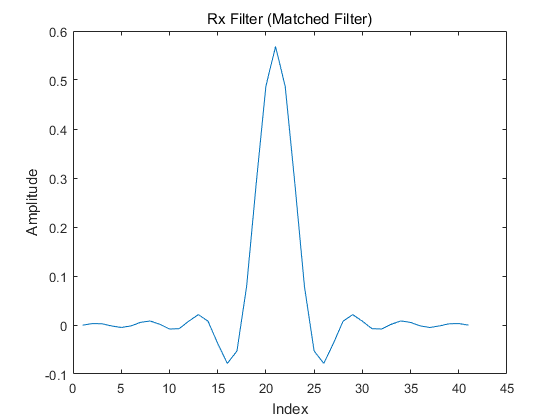
收发端滤波器的整体响应和过零点：

Channel

为了便于说明， 我们先忽略channel中的AWGN， 并且增加一定的延时（比如一个采样间隔）， 注意这里的采样间隔并不等同于符号间隔：

1
2
3
timeOffset = 1; % Delay (in samples) added
% Delayed sequence
rxDelayed = [zeros(1, timeOffset), txSequence(1:end-timeOffset)];

Receiver

  1. 没有符号同步的情况：

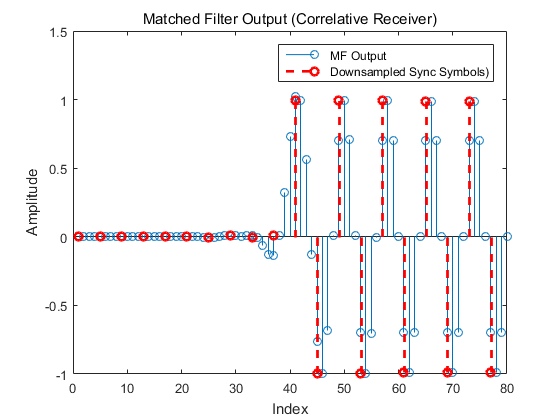
我们先假设接收机中没有符号的定时同步，那么经过match filter收端收到的符号就是：

1
2
3
4
5
6
mfOutput = filter(hrx, 1, rxDelayed); % Matched filter output
figure
stem(mfOutput)
title('Matched Filter Output (Correlative Receiver)')
xlabel('Index')
ylabel('Amplitude')

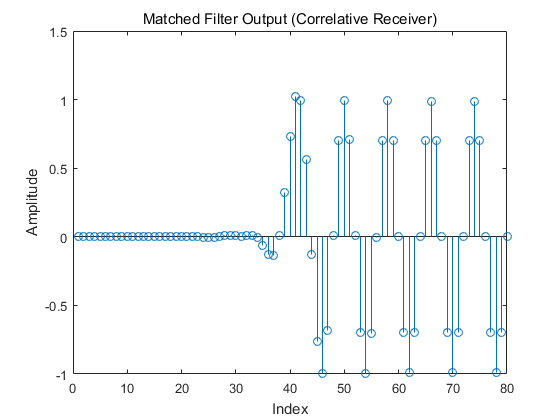
针对MF 输出， 任意选择sample送给符号判决器：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
rxSym = downsample(mfOutput, L);

% Generate a vector that shows the selected samples
selectedSamples = upsample(rxSym, L);
selectedSamples(selectedSamples == 0) = NaN;

% And just for illustration purposes
figure
stem(mfOutput)
hold on
stem(selectedSamples, '--r', 'LineWidth', 2)
title('Matched Filter Output (Correlative Receiver)')
xlabel('Index')
ylabel('Amplitude')
legend('MF Output', 'Downsampled Sequence (Symbols)')
hold off

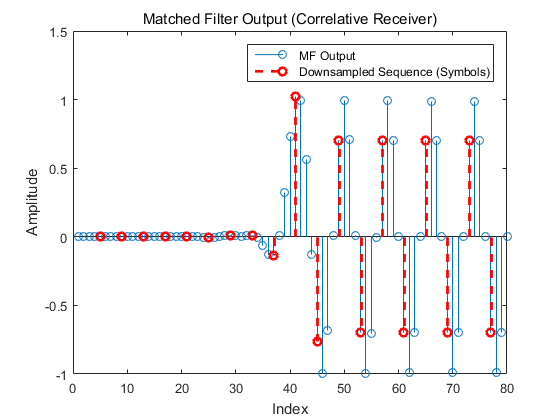
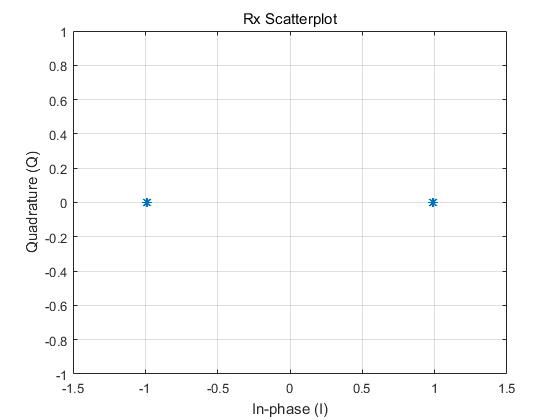
最后， 画出接收符号的散点图：

1
2
3
4
5
6
7
figure
plot(complex(rxSym(rcDelay+1:end)), 'o')
grid on
xlim([-1.5 1.5])
title('Rx Scatterplot')
xlabel('In-phase (I)')
ylabel('Quadrature (Q)')

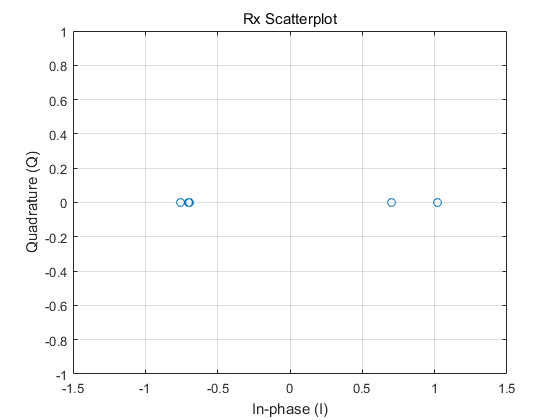
可以看出接收的符号已经偏离了+1 和 -1

  1. 有符号同步的情况

在downsample 函数中增加一个TimeOffset的值：

1
rxSym = downsample(mfOutput, L, timeOffset);

这种情况下， 被选择的符号就是：

1
2
3
4
5
6
7
8
9
10
11
12
13
selectedSamples = upsample(rxSym, L);
selectedSamples(selectedSamples == 0) = NaN;

% And just for illustration purposes
figure
stem(mfOutput)
hold on
stem(selectedSamples, '--r', 'LineWidth', 2)
title('Matched Filter Output (Correlative Receiver)')
xlabel('Index')
ylabel('Amplitude')
legend('MF Output', 'Downsampled Sequence (Symbols)')
hold off

画出散点图：

TED 设计

本部分我们讨论Timing Error的检测.。

TED 中的一种是最大似然检测， 即（ML-TED）， 这种检测器使用的是微分式的匹配滤波器：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
h = [0.5 0 -0.5]; % central-differences kernel function
central_diff_mf = conv(h, hrx);

% Skip the kernel delay
dmf = central_diff_mf(2:1+length(hrx));

figure
plot(hrx, '-*')
hold on, grid on
plot(dmf, '-r>')
legend('MF', 'dMF')
title('MF vs. dMF')
xlabel('Index')
ylabel('Amplitude')
hold off

可以看到dMF响应的零点对应MF 响应的peak点。

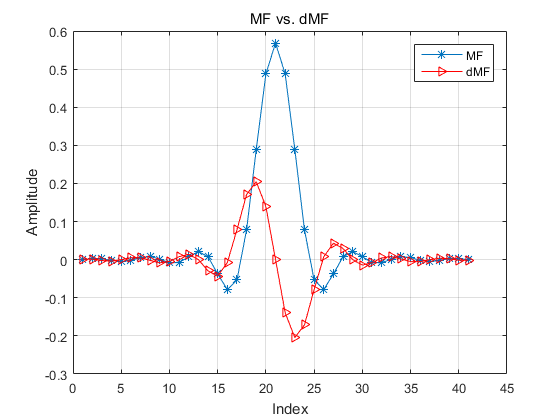
ML-TED

那么经过dMF后， 下采样的sample为：

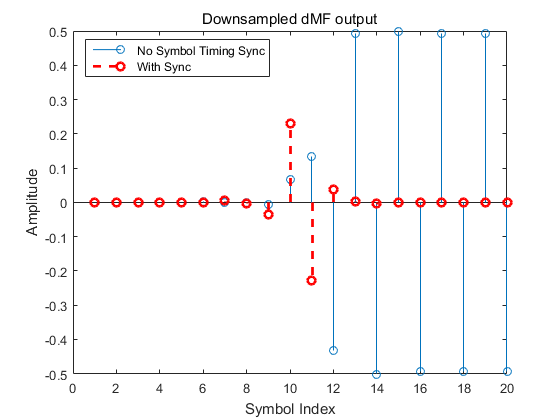
计算timing error：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
% First do PAM-demodulation
rxdata_nosync   = pamdemod(downsample(mfOutput, L), M);
rxdata_withsync = pamdemod(downsample(mfOutput, L, timeOffset), M);
% Then, regenerate the corresponding constellation symbols
decSym_nosync   = real(pammod(rxdata_nosync, M));
decSym_withsync = real(pammod(rxdata_withsync, M));

% TED Output
e_nosync       = decSym_nosync .* dmfDownsampled_nosync;
e_withsync     = decSym_withsync .* dmfDownsampled_withsync;

% And just for illustration purposes
figure
stem(e_nosync)
hold on
stem(e_withsync, '--r', 'LineWidth', 2)
xlabel('Symbol Index')
ylabel('Amplitude')
legend('No Symbol Timing Sync', 'With Sync')
title('ML-TED Output - Timing Errors')
hold off

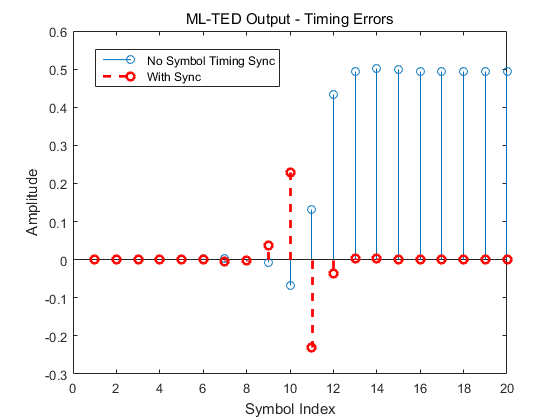
从图中可以看出， 当receiver 不知道TimeOffset的信息时， TED的输出有较大的幅值， 因此可以利用这个误差值来获取同步。

但是需要注意的是， ML-TED要求发端发送固定的pattern， +1 ， -1， +1， -1等。 当发送的是随机的symbol时候， ML-TED的输出就会有很多噪声， 影响timing loop稳定性。

ZC-TED（Zero-Crossing）

Zero-crossing 方法的timing error检测不需要dMF， 只需要MF输出的sample。因为每两个symbol 之间有L-1的sample， 当MF的输出存在极性转换时（+1 —> -1），就可以用中间这个sample的值作为TED的输出：

以下图为例， MF的输出从+1 到 -1 转换时， 可以取 Index = 3的sample作为TED的输出：

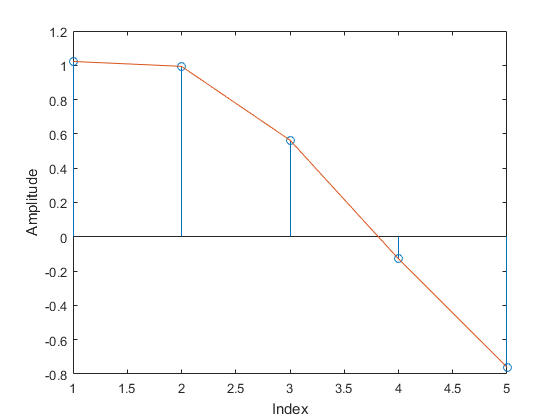
那么据此， 可以得到ZC-TED的输出：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
% Midpoint samples
midSamples_nosync     = mfOutput((L/2 + 1):L:end);
midSamples_withsync   = mfOutput((L/2 + 1 + timeOffset):L:end);

% Sign correction values based on symbol decisions:
signcorrection_nosync   = [-diff(decSym_nosync), 0];
signcorrection_withsync = [-diff(decSym_withsync), 0];
% Note: the padded zero is just for the signcorrection vector
% to have a length equivalent to the the vector of midsamples.

% ZC-TED output:
zcted_nosync   = midSamples_nosync .* signcorrection_nosync;
zcted_withsync = midSamples_withsync .* signcorrection_withsync;

% Plot
figure
stem(zcted_nosync)
hold on
stem(zcted_withsync, '--r', 'LineWidth', 2)
hold off
xlabel('Symbol Index')
ylabel('Amplitude')
legend('No Symbol Timing Sync', 'With Sync')
title('ZC-TED Output - Timing Errors')

如下图所示：

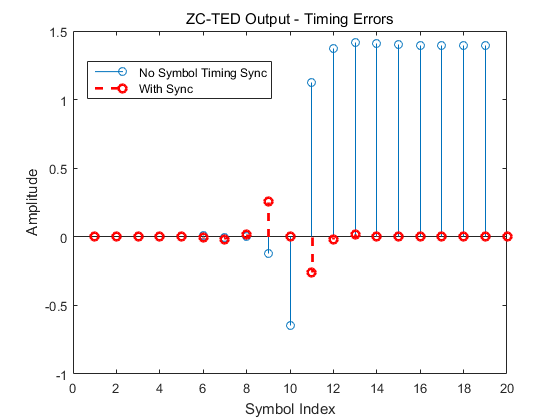
参考文献

[1] http://igorfreire.com.br/symbol-timing-synchronization-tutorial/#wireless-communications-fpga-course

[2] Rice, Michael. Digital Communications: A Discrete-Time Approach. Upper Saddle River, NJ: Prentice Hall, 2009