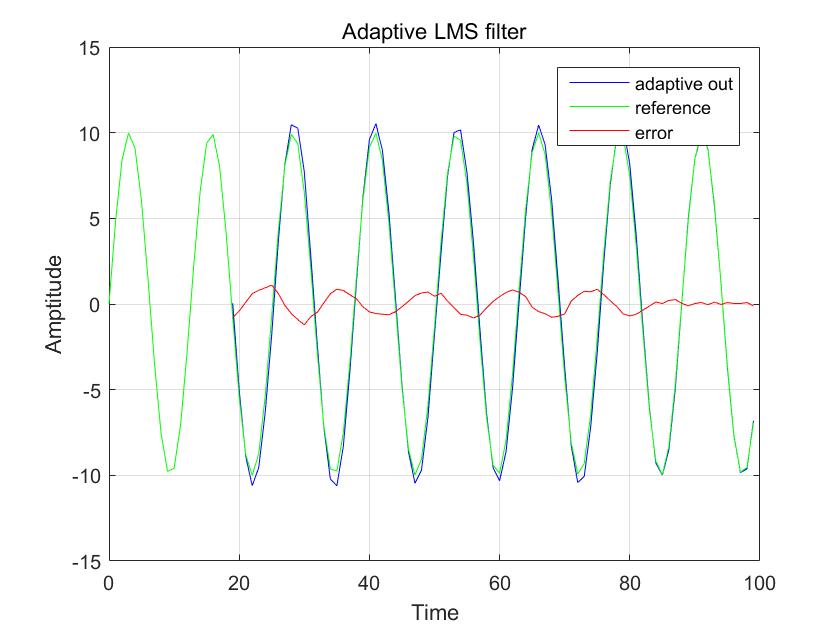
本篇主要介绍Adapter Filter中常见的一种算法LMS（Least Mean Square），常用于噪声消除，通信上的信道均衡等。

LMS算法简介

如下图所示是一个N-tap的自适应滤波器：

$y(n) = \sum_{i=0}^{N-1} w_i(n) x(n-i)$

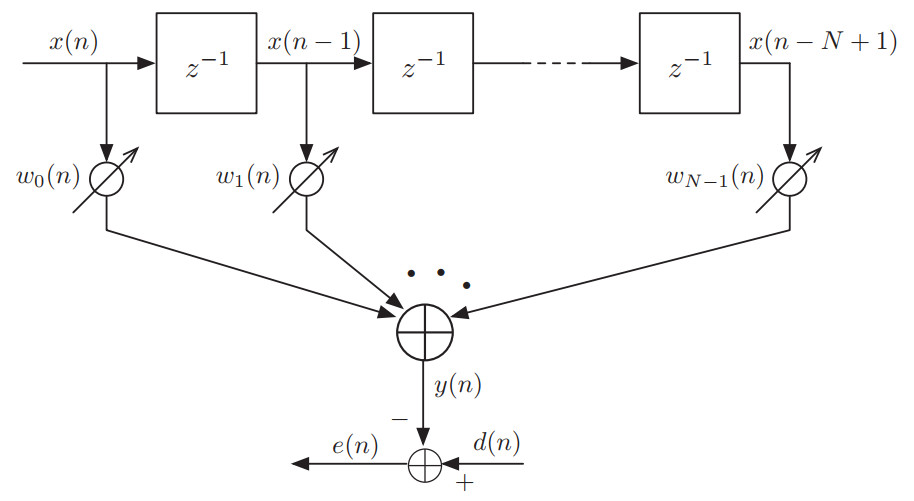
输入信号是x(n)，参考输出是d(n)，滤波器的输出是y(n).

滤波器的输出误差就是：

$e(n) = d(n) - y(n)$

滤波器的tap系数是随时间变化的，即 adaptive。 LMS算法依据的准则就是使得参考输出和滤波器实际输出之间的均方差最小。那么代价函数可以写成

$\varepsilon = E[e^2(n)]$

也就是：

$\begin{align*} \varepsilon &= E \{ [d(n) - \mathbf{W}^T(n) \mathbf{X}(n) ]^2\} \\ &= E[d^2(n)] - 2E[d(n) \mathbf{W}^T(n) \mathbf{X}(n) ] + E[ \mathbf{W}^T(n) \mathbf{X}(n)\mathbf{X}^T(n) \mathbf{W}(n)] \end{align*}$

利用steepest-descent算法，沿着性能曲面最速下降方向（负梯度方向）调整滤波器强权向量，搜索性能曲面的最小点，计算权向量的迭代公式为 :

$\mathbf{W}(n+1) = \mathbf{W} (n) - \mu \nabla \varepsilon$

$\mu$是步长因子，传统的LMS算法实际上是steepest-descent算法的一种简化实现：代价函数变成：$\varepsilon = e^2(n)$

那么tap系数向量的迭代公式变成：

$\mathbf{W}(n+1) = \mathbf{W} (n) - \mu \nabla e^2(n)$

其中$\nabla$代表的是梯度函数，并且是以列向量的方式表示：

$\nabla = [\frac{\partial}{\partial w_0}, \; \frac{\partial}{\partial w_1}, \; \dots \; \frac{\partial}{\partial w_{N-1}} ]$

那么注意第i项：

$\frac{\partial e^2(n)}{\partial w_i} = 2e(n) \frac{\partial e(n)}{\partial w_i} = -2e(n) \frac{\partial y(n)}{\partial w_i}$

上式中，没有d(n)项，是因为d(n)和tap系数不想关，把第一个公式带入上面的公式有：

$\frac{\partial e^2(n)}{\partial w_i} = -2e(n)x(n-i)$

LMS 算法总结

根据上面所述，LMS算法可以总结如下：

LMS 算法实例

首先创建一个lms算法的函数：

function [yn,W,en]=lms_func(xn,dn,M,mu,itr)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Input:
%     xn   input signal-colum vecot
%     dn   refrence response signal vertor
%     M    order of filter
%     mu   step factor, require >0   
%     itr   iteration times
% Output:
%     W    fiter taps matrix :  M X iter
%     en   Error colum vector: iter X 1 
%     yn   filter output colum vector
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
if nargin == 4                  
    itr = length(xn);
elseif nargin == 5             
    if itr>length(xn) || itr<M
        error('ERROR: iteration times maybe too large or small!');
    end
else
    error('please check the inpur paramter of this function!');
end
en = zeros(itr,1);             
W  = zeros(M,itr);             
% Iterative caculation
for k = M:itr                 
    x = xn(k:-1:k-M+1);   
    y = W(:,k-1).' * x;     
    en(k) = dn(k) - y ;    
    
    W(:,k) = W(:,k-1) + 2*mu*en(k)*x;
end
% filter output sequce
yn = inf * ones(size(xn));
for k = M:length(xn)
    x = xn(k:-1:k-M+1);
    yn(k) = W(:,end).'* x;
end

下面是一个实例

close  all; clear
%  signal generation
t=0:99;
xs=10*sin(0.5*t);
% generate random noise
randn('state',sum(100*clock));
xn=randn(1,100);
% Adative filter
xn = xs+xn;
xn = xn.' ;   % filter inpput
dn = xs.' ;   % referce signal
M  = 20   ;   % fiter order
rho_max = max(eig(xn*xn.'));   % The max Eiggen value of correlative matrix
mu = rand()*(1/rho_max)   ;    % step factor
[yn,W,en] = lms_func(xn,dn,M,mu);
% draw figures
figure;
subplot(2,1,1);
plot(t,xn);grid;
ylabel('Amptitude');
xlabel('Time');
title('{Filter input signal}');
% draw filter output
subplot(2,1,2);
plot(t,yn);grid;
ylabel('Amptitude');
xlabel('Time');
title('{Adaptive filter output signal}');
% Compare figure
figure 
plot(t,yn,'b',t,dn,'g',t,dn-yn,'r');grid;
legend('adaptive out','reference','error');
ylabel('Amptitude');
xlabel('Time');
title('{Adaptive LMS filter}');

运行结果如下：

filter 输入和输出

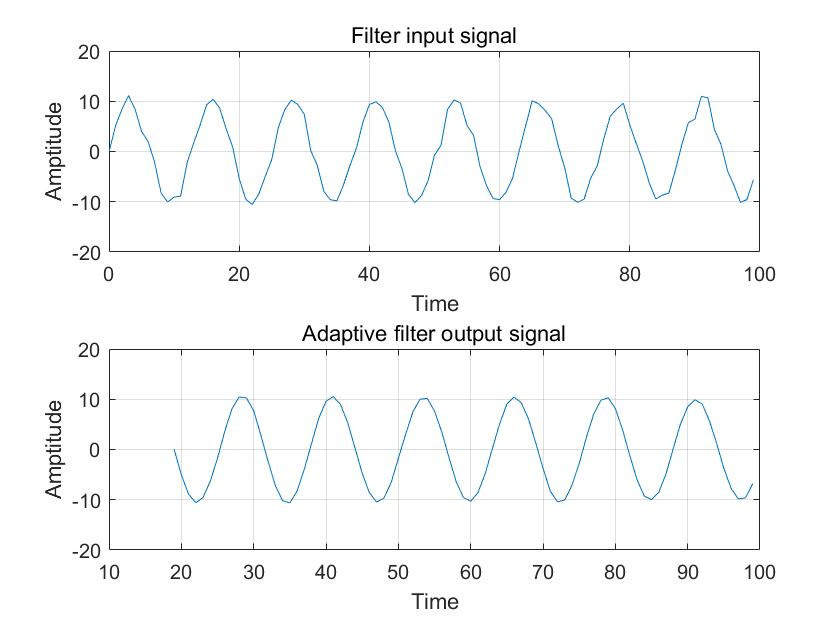
输入输出对比和误差