Tanner 图

LDPC码的校验矩阵可以用tanner graph来表示，如下图所示：

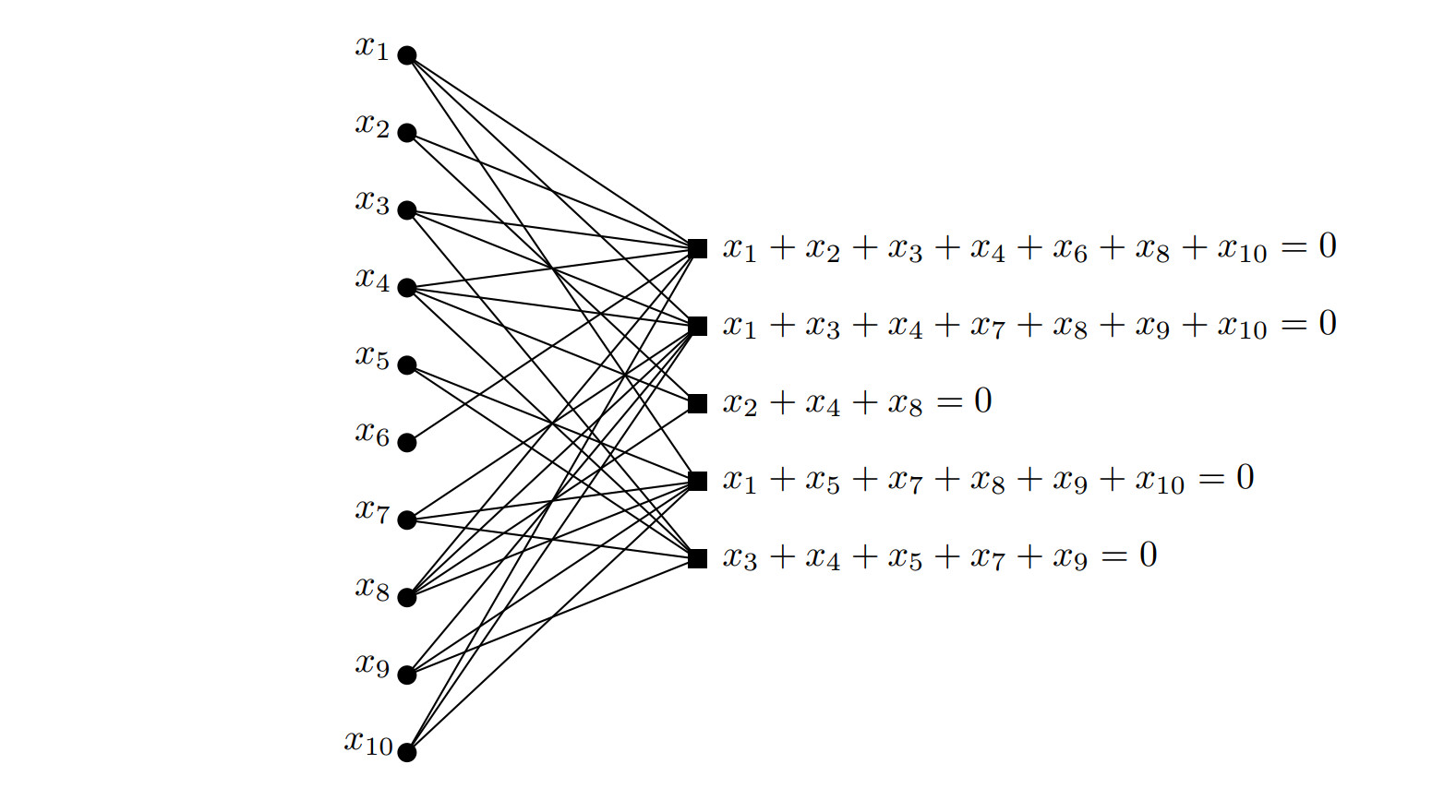
图中的左侧是信息节点（message nodes），代表的一个码字中的bit个数，右侧则是校验节点。

sum-product解码算法

sum-product解码算法的目的是计算最大的后验概率（maximum a posteriori probability）即：

$P_i = P\{c_i =1| N\}$

上面的式子表示的是所有的校验等式都满足的情况下，码字中第 i bit等于1的概率。假设bit信息相互独立，我们希望计算下面的概率：

$Pr\{c_1\oplus c_2 \dots\oplus c_k|y_1,\dots y_k\}$

假设：

$p = 2Pr\{c_1 = 0|y_1\} - 1; \quad q = 2Pr\{c_2 = 0|y_2\} - 1$

那么有：

$2Pr\{c_1 \oplus c_2= 0|y_1, y_2\} - 1 = p q$

所以要计算的概率是：

$2Pr\{c_1\oplus c_2 \dots\oplus c_k|y_1,\dots y_k\}-1 = \prod_{i=1}^{k}(2Pr\{c_i=0| y_i\} -1)$

假设：

$L\{c_i|y_i\} = \frac {Pr \{c_i = 0|y_i\}} {Pr\{c_i = 1|y_i \} }$

所以：

$Pr \{c_i = 0|y_i\} = \frac {L(c_i | y_i)} {1+ L (c_i | y_i)}$

进一步化简, 其中$l_i=lnL(c_i|y_i)$：

$2 Pr \{c_i = 0|y_i\} - 1 = \frac {L-1} {L+1} = tanh (l/2)$

那么从校验节点到信息节点输出的外信息是：

$E_{j,i} =lnL\{c_1\oplus c_2 \dots\oplus c_k|y_1,\dots y_k\} = ln \frac {1+ \prod_{i=1}^{k}tanh(l_1/2)} {1- \prod_{i=1}^{k}tanh(l_1/2)}$

sum-product解码算法实际上是一个迭代的过程：首先从bit节点获得每个bit的先验信息，然后根据上式计算校验节点输出的外信息，然后不断的迭代，直到校验等式全部满足。

假设发送的code word是$\textbf{c} = [0 \;0 \;1 \;0 \;1 \;1],]$, 接收到的码字是$\textbf{y} = [1\; 0 \;1 \;0 \;1 \;1]$。并且假设发送0收到1的概率为1，那么可以计算先验LLR为：

$\textbf{r} = [−1.3863, 1.3863,−1.3863, 1.3863,−1.3863,−1.3863].$

比如下面的tanner graph，解码算法的第一步是初始化信息节点的bit LLR；

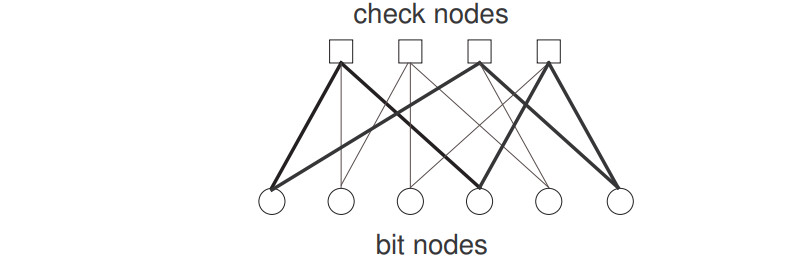
第一个bit包含1、3校验节点的信息，所以初始化LLR为：

$M_{1,1} = r_1 = -1.3863, \quad M_{3,1} = r_1 = -1.3863$

同理，其他的bit LLR也可以初始化：

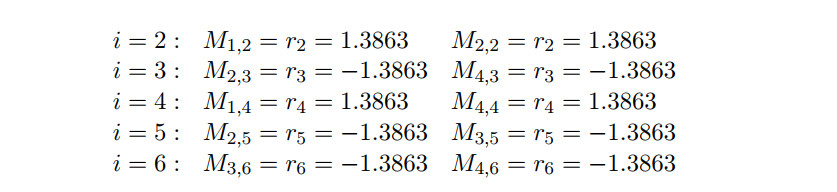
第二步就进入一个迭代的过程，信息在校验节点和信息节点之间来回更新。先更新校验节点的外信息，也就是前文中的$E_{j,i}$, 其中的j代表的是校验节点（check nodes）而i代表的是信息节点（message nodes）。

由于第一个校验节点包含1、2、4bit的信息，那么根据上文中的公式计算，更新LLR：

同理可以计算其他项，更新后的LLR 矩阵为：

所以第一次迭代后，我们可以计算出第一个bit总的LLR，是外信息和来自信道内信息的和：

$L_1 = r_1 + E_{1.1} + E_{3,1} = 0.1213$

剩余bit的总LLR信息是：

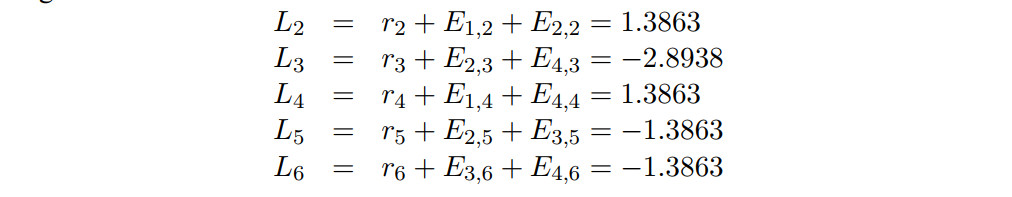
硬判决后的bit是$\textbf{z} = [0\;0\;1\;0\;1\;1]$, 在判断是否满足校验等式：

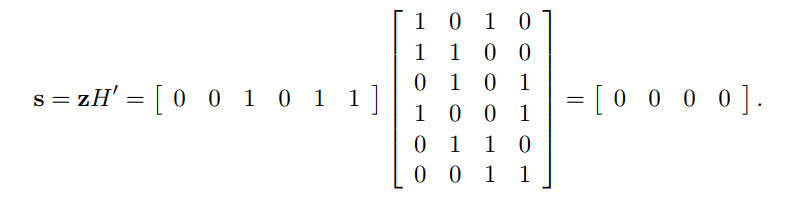
校验等式满足，迭代终止，那么硬判决的bit就是解码输出bit