LDPC简介（一）

本篇主要介绍一下LDPC算法的基础内容。

LDPC实际上是一种线性码。如果一个码字（code word）用多个等式校验，那么这些等式可以写成矩阵运算的形式：

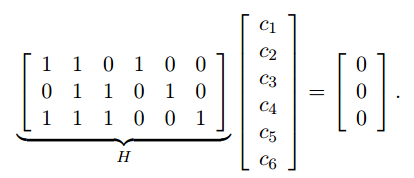
矩阵H就是校验矩阵，每一行就是一个校验等式，所以也可以写成下面的形式：

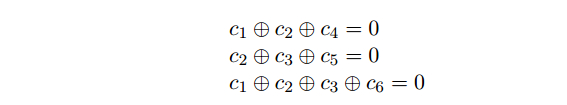
如果对于一个码字, 我们要区分信息bit和校验bit，假设下面这个code word，信息bit是c1, c2, c3

$\textbf{y} = \{c_1\; c_2\; c_3 \; c_4\; c_5\;c_6 \}$

那么就可以把校验等式重新写成：

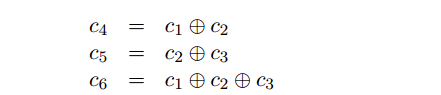
如果用矩阵的形式表示就是：

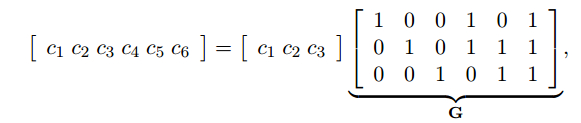
矩阵$\textbf{G}$就是码字的生成矩阵，如果一个code word的长度是n，信息bit是k，那么这个编码的码率就是

k/n。在本例中码率是3/6=1/2。

生成矩阵和校验矩阵存在一定的联系，如果校验矩阵是$\textbf{H}$，那么可以通过高斯消元法简化成下面的形式：

$\textbf{H} = [\textbf{A}\; \textbf{I}_{n-k}]$

那么生成矩阵$\textbf{G}$就可以写成：

$\textbf{G} = [\textbf{I}_k\; \textbf{A}^T]$

在上面的例子中，假设传输的码字是$\textbf{c}=\lbrace1 \;0 \;1 \;1 \;1 \;0\rbrace$, 接收到的码字是$\textbf{y}=\lbrace1 \;0 \;1 \;0 \;1 \;0 \rbrace$。那么就可以通过校验矩阵检测出错误bit：

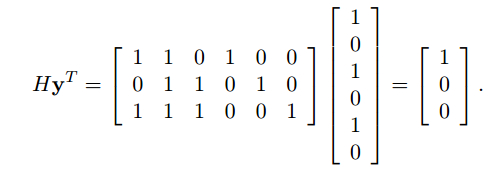
但是如果有3bit错了，比如收到的是：$\textbf{y}=\lbrace 0 \;0 \;1 \;0 \;1 \;1\rbrace $那么这个校验矩阵就检测不出来了。

因为错误的bit数目大于了码字的最小Hanmming距离。

LDPC编码相较于传统的线性分组码的特点是校验矩阵$\textbf{H}$是稀疏的（spare），并且在解码算法上有差别。

下一篇在介绍解码算法。