信号的向量表示

发表于 | 分类于

离散信号可以用向量来表示，这就和线性代数联系的较为紧密.

如何表示2个信号的相似程度呢？通过向量类比，可以求向量之间的夹角，如果夹角趋近于180说明2个信号差异越大，如果夹角趋近于0，说明2个信号越相似

比如下面的例子：

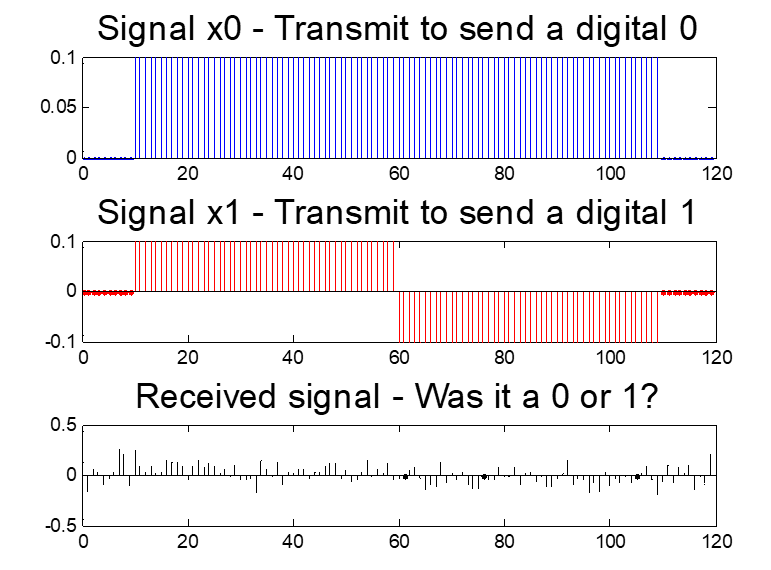
There are two possible signals that can be sent, x0 or x1, which communicate a transmitted 0 or 1, respectively. The code randomly picks one of the signals, and then adds noise to it. Using inner products (which the code computes), you can guess which signal was sent.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
%%%
N = 120;
n = 0:N-1;
x0 = [zeros(10,1); ones(100,1); zeros(10,1)];
x0 = x0/norm(x0);
x1 = [zeros(10,1); ones(50,1); -ones(50,1); zeros(10,1)];
x1 = x1/norm(x1);
signals=[x0,x1];
subplot(311)
stem(n,x0,'b','Marker','none','LineWidth',1)
title('Signal x0 - Transmit to send a digital 0','fontsize',18)
subplot(312)
stem(n,x1,'r','Marker','none','LineWidth',1)
title('Signal x1 - Transmit to send a digital 1','fontsize',18)

% received signal is either x0 or x1 with additive noise
y = signals(:,round(rand(1,1))+1) + 0.2*randn(size(x1));
y=y./norm(y); % normalize y
        
subplot(313)
stem(n,y,'k','Marker','none','LineWidth',1)
title('Received signal - Was it a 0 or 1?','fontsize',18)

% computes the inner products between y and both x0 and x1:
innerproduct0  = abs( y' * x0 )
innerproduct1  = abs( y' * x1 )

信号处理实际上是矩阵处理，特别是对于离散系统而言